What is the other Incorrectness logic?

Posted on by John Wickerson

The Hoare triple \{P\}\,c\,\{Q\} has a very simple meaning, namely:

\forall\sigma, \sigma'\ldotp \sigma \in P \wedge (\sigma,\sigma') \in c \longrightarrow \sigma'\in Q.

That is: if the precondition P is satisfied in some state \sigma, and c can transform \sigma into \sigma', then \sigma' must satisfy the postcondition Q. (We’ll allow non-deterministic commands, so \sigma' need not be uniquely determined by c and \sigma.) Or, more concisely: if P holds before executing c, then Q will hold afterwards.

The statement above can be reformulated in a couple of different ways, all equivalent. One way is to introduce Dijkstra’s concept of a weakest precondition, like so:

pre(c,Q) = \{\sigma\mid \forall \sigma'\ldotp (\sigma,\sigma') \in c \longrightarrow \sigma'\in Q\}

and then observe that \{P\}\,c\,\{Q\} is the same as P \subseteq pre(c,Q). Another way is to introduce the concept of a strongest postcondition, also due to Dijkstra, like so:

post(P,c) = \{\sigma'\mid \exists \sigma\ldotp \sigma\in P \wedge (\sigma,\sigma') \in c\}

and then observe that \{P\}\,c\,\{Q\} is the same as post(P,c) \subseteq Q.

◆

In 2019, O’Hearn introduced Incorrectness logic. This logic involves triples [P]\,c\,[Q] that have a subtly different meaning to Hoare’s, namely:

\forall\sigma'\ldotp \sigma' \in Q \longrightarrow \exists \sigma\ldotp \sigma \in P \wedge (\sigma,\sigma') \in c.

That is: if the postcondition Q is satisfied by some state \sigma', then there must exist some state \sigma that can be transformed into \sigma' by command c and that satisfies the precondition P. Or, more concisely: every state where Q holds is reachable by executing c from a state where P holds.

There’s a neat duality between Incorrectness logic and Hoare logic:

\{P\}\,c\,\{Q\} is equivalent to post(P,c) \subseteq Q

[P]\,c\,[Q] is equivalent to post(P,c) \supseteq Q

What’s curious is that this \subseteq/\supseteq trick can only be used with the strongest-postcondition formulation. If you try it on the weakest-precondition formulation, you don’t get Incorrectness logic. In other words, P \subseteq pre(c,Q) and post(P,c) \subseteq Q are logically equivalent, but P \supseteq pre(c,Q) is not the same as post(P,c) \supseteq Q. If post(P,c) \supseteq Q corresponds to Incorrectness logic, then what does P \supseteq pre(c,Q) correspond to?

◆

So let’s see what happens if we introduce a third type of triple, \langle P\rangle\,c\,\langle Q\rangle, which shall mean:

\forall \sigma\ldotp (\forall \sigma' (\sigma,\sigma') \in c \longrightarrow \sigma' \in Q) \longrightarrow \sigma \in P.

That is: if \sigma is a state that is always transformed by command c into one that satisfies the postcondition Q, then \sigma must satisfy the precondition P. Or, more concisely: if P doesn’t hold before executing c, then Q will not hold afterwards.

Essentially, we are filling in the gap marked “???” in the picture below (where the thick arrows indicate equivalences):

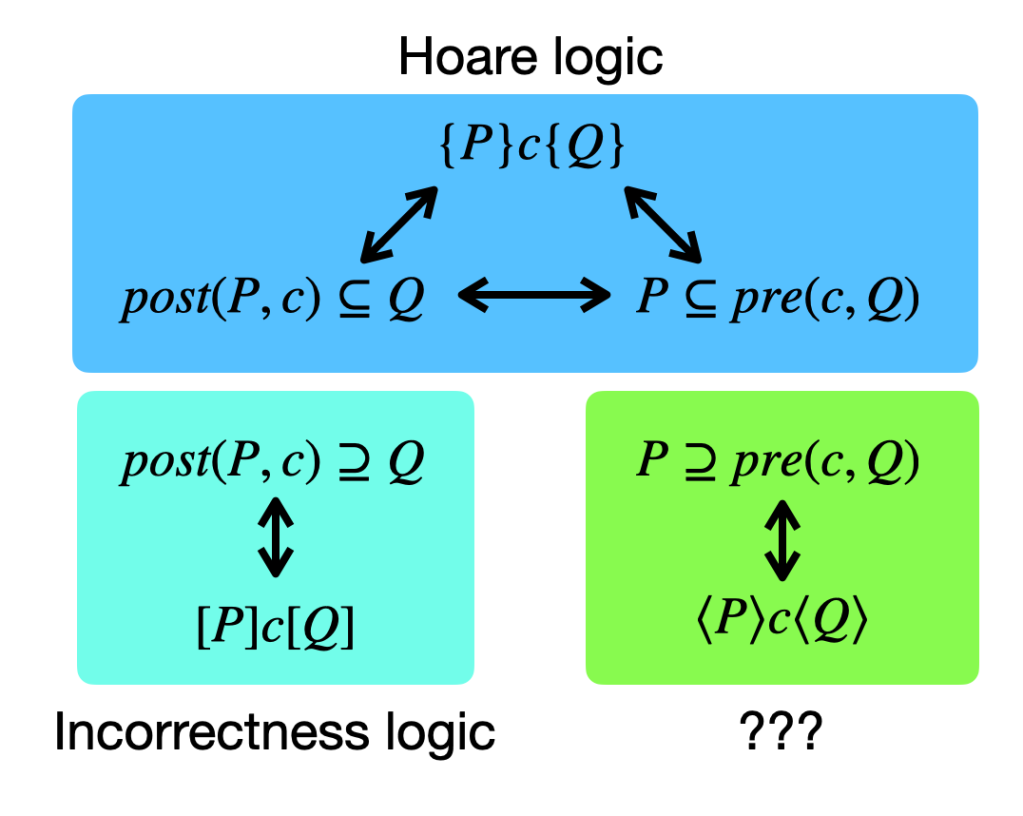
What can we say about these new \langle P \rangle c \langle Q \rangle triples? What properties do they enjoy?

In some ways, all three forms of triple are alike. For instance, they all admit the same Sequencing rule:

\displaystyle\frac{ \{ P \} c_1 \{ Q \} \quad \{ Q \} c_2 \{ R \} } { \{ P \} c_1 ; c_2 \{ R \} }

\displaystyle\frac{ [ P ] c_1 [ Q ] \quad [ Q ] c_2 [ R ] } { [ P ] c_1 ; c_2 [ R ] }

\displaystyle\frac{ \langle P \rangle c_1 \langle Q \rangle \quad \langle Q \rangle c_2 \langle R \rangle } { \langle P \rangle c_1 ; c_2 \langle R \rangle }

and they all admit the Iteration rule:

\displaystyle\frac{ \{ P \} c \{ P \} } { \{ P \} c^* \{ P \} }  \displaystyle\frac{ [ P ] c [ P ] } { [ P ] c^* [ P ] }  \displaystyle\frac{ \langle P \rangle c \langle P \rangle } { \langle P \rangle c^* \langle P \rangle }

In some ways, the new triples behave more like Incorrectness triples than like Hoare triples. This is the case for the Skip rules:

\displaystyle\frac{ P \Rightarrow Q } { \{ P \} \text{skip} \{ Q \} }  \displaystyle\frac{ Q \Rightarrow P } { [ P ] \text{skip} [ Q ] }  \displaystyle\frac{ Q \Rightarrow P } { \langle P \rangle \text{skip} \langle Q \rangle }

and for the Consequence rules:

\displaystyle\frac{ P' \Rightarrow P \quad \{ P \} c \{ Q \} \quad Q \Rightarrow Q' } { \{ P' \} c \{ Q' \} }

\displaystyle\frac{ P \Rightarrow P' \quad [ P ] c [ Q ] \quad Q' \Rightarrow Q } { [ P' ] c [ Q' ] }

\displaystyle\frac{ P \Rightarrow P' \quad \langle P \rangle c \langle Q \rangle \quad Q' \Rightarrow Q } { \langle P' \rangle c \langle Q' \rangle }

In yet other ways, all three forms of triple are different. For instance, they all say different things about the command \varnothing that always diverges (fails to terminate):

  • \{ P \} \varnothing \{ Q \} always holds, because Hoare logic gives no guarantees about non-terminating executions.
  • [ P ] \varnothing [ Q ] holds iff Q = False, because Incorrectness logic demands termination.
  • \langle P \rangle \varnothing \langle Q \rangle holds iff P = True, because \varnothing will always fail to reach Q.

Another way to distinguish the three forms is to ask what they say when the postcondition is unsatisfiable. (In what follows, let diverges(c) be the set of states from which execution of c diverges.)

  • \{ P \} c \{ False \} holds iff P \Rightarrow diverges(c); i.e. P is a sufficient condition for c diverging.
  • [ P ] c [ False ] always holds.
  • \langle P \rangle c \langle False \rangle holds iff diverges(c) \Rightarrow P; i.e. P is a necessary condition for c diverging.

Here are some rules about c_1 \cup c_2, which denotes a non-deterministic choice between commands c_1 and c_2:

\displaystyle\frac{ \{ P_1 \} c_1 \{ Q_1 \} \quad \{ P_2 \} c_2 \{ Q_2 \} } { \{ P_1 \wedge P_2 \} c_1 \cup c_2 \{ Q_1 \vee Q_2 \} }

\displaystyle\frac{ [ P_1 ] c_1 [ Q_1 ] \quad [ P_2 ] c_2 [ Q_2 ] } { [ P_1 \vee P_2 ] c_1 \cup c_2 [ Q_1 \vee Q_2 ] }

\displaystyle\frac{ \langle P_1 \rangle c_1 \langle Q_1 \rangle \quad \langle P_2 \rangle c_2 \langle Q_2 \rangle } { \langle P_1 \wedge P_2 \rangle c_1 \cup c_2 \langle Q_1 \wedge Q_2 \rangle }

Here are some rules for conjoining or disjoining two different specifications for the same command:

\displaystyle\frac{ \{ P_1 \} c \{ Q_1 \} \quad \{ P_2 \} c \{ Q_2 \} } { \{ P_1 \vee P_2 \} c \{ Q_1 \vee Q_2 \} }

\displaystyle\frac{ \{ P_1 \} c \{ Q_1 \} \quad \{ P_2 \} c \{ Q_2 \} } { \{ P_1 \wedge P_2 \} c \{ Q_1 \wedge Q_2 \} }

\displaystyle\frac{ [ P_1 ] c [ Q_1 ] \quad [ P_2 ] c [ Q_2 ] } { [ P_1 \vee P_2 ] c [ Q_1 \wedge Q_2 ] }

\displaystyle\frac{ \langle P_1 \rangle c \langle Q_1 \rangle \quad \langle P_2 \rangle c \langle Q_2 \rangle } { \langle P_1 \wedge P_2 \rangle c \langle Q_1 \wedge Q_2 \rangle }

Here are some ways to translate between Hoare triples and Incorrectness triples. (In what follows, let determ(c) be the set of states from which execution of c is deterministic, and let c^{-1} denote the inverse of the command c.)

  • If P \cap diverges(c) = \emptyset then \{ P \} c \{ Q \} implies [Q] c^{-1} [P].
  • If P \subseteq determ(c) then [Q] c^{-1} [P] implies \{ P \} c \{ Q \}.
  • Hence, if P \cap diverges(c) = \emptyset and P \subseteq determ(c) then \{ P \} c \{ Q \} coincides with [Q] c^{-1} [P].

Here are some ways to translate between Hoare triples and the new form of triples.

  • If P \cap diverges(c) = \emptyset then \{ P \} c \{ Q \} implies \langle \neg P \rangle c \langle \neg Q \rangle.
  • If P \subseteq determ(c) then \langle \neg P \rangle c \langle \neg Q \rangle implies \{ P \} c \{ Q \}.
  • Hence, if P \cap diverges(c) = \emptyset and P \subseteq determ(c) then \{ P \} c \{ Q \} coincides with \langle \neg P \rangle c \langle \neg Q \rangle.

If we become a bit more concrete now, and model program states simply as functions from variables to integers, then we can obtain specifications of the “increment x” command like so:

  • \{ x = n \}\,{+}{+}x \,\{x = n + 1\}
  • [ x = n ] \, {+}{+}x \, [ x = n + 1 ]
  • \langle x = n \rangle \, {+}{+}x \, \langle x = n + 1 \rangle

or:

  • \{ x > n \} \, {+}{+}x \, \{x > n + 1\}
  • [ x > n ] \, {+}{+}x \, [ x > n + 1 ]
  • \langle x > n \rangle \, {+}{+}x \, \langle x > n + 1 \rangle

For specifying an “assign a constant” command, we can use:

  • \{ x > 2 \} \, x := 5 \, \{ x = 5 \}
  • [ x > 2 ] \, x := 5 \, [ x = 5 ]

but \langle x > 2 \rangle \, x := 5 \, \langle x = 5 \rangle is invalid because x>2 is not necessary to guarantee x = 5 after the assignment. In fact, any initial state will suffice here, which means \langle True \rangle \, x := 5 \, \langle x = 5 \rangle is valid.

We can also specify that assignment command more loosely:

  • \{ x > 2 \} \, x := 5 \, \{ x > 3 \}

but [ x > 2 ] \, x := 5 \, [ x > 3 ] is invalid because executing x := 5 can never reach a final state where x = 7, say. And \langle x > 2 \rangle \, x := 5 \, \langle x > 3 \rangle is invalid too, for the same reason as given above.

Finally, we can specify some non-deterministic commands, such as a command that assigns to x either 4 or 5:

  • \{ True \} \, (x := 4) \cup (x := 5) \, \{ x = 4 \vee x = 5 \}
  • [ True ] \, (x := 4) \cup (x := 5) \, [ x = 4 \vee x = 5 ]
  • \langle True \rangle \, (x := 4) \cup (x := 5) \, \langle x = 4 \vee x = 5 \rangle

or a command that either increments x or does nothing:

  • \{ x > n \} \, ({+}{+}x) \cup \text{skip} \, \{ x > n \}
  • [ x > n ] \, ({+}{+}x) \cup \text{skip} \, [ x > n ]
  • \langle x > n \rangle \, ({+}{+}x) \cup \text{skip} \, \langle x > n \rangle

◆

In terms of related work:

  • O’Hearn does mention the curious inequivalence between P \supseteq pre(c,Q) and post(P,c) \supseteq Q in his POPL’19 paper (near the end of Section 7), but doesn’t dig into the implications of building a proof system around triples that mean P \supseteq pre(c,Q).
  • He does, however, point out some earlier work by Cousot et al. that made use of these triples in an automated verification context, which was published in VMCAI 2013. Cousot et al. referred to them as necessary preconditions, and they used them because they wanted to avoid false positives in their automatic tool. However, they didn’t develop a set of proof rules for reasoning about these triples.
  • More recently, Zilberstein, Dreyer, and Silva’s OOPSLA 2021 paper proposes Outcome logic as a way to unify \{P\}\,c\,\{Q\} triples and [P]\,c\,[Q] triples into a single logic based on monads and monoids. I haven’t yet figured out whether Outcome logic also covers \langle P\rangle \,c\,\langle Q\rangle triples.

To conclude: \langle P\rangle \,c\,\langle Q\rangle gives rise to a proof system that seems to have some interesting properties, and perhaps it shines some light on the nature of Hoare logic and Incorrectness logic by where it differs from them. I’m not convinced that it’s a useful proof system like Hoare logic or Incorrectness logic certainly are. Still, it’s always satisfying to fill in “gaps”!

An Isabelle-2023 proof script that formalises all of the results given above is available.

2 thoughts on “What is the other Incorrectness logic?”

  2. Very nice post!

    In terms of related work: Predating Ascari et al., Zhang & Kaminski also suggests the logic “???” (and others) and – funnily enough – also call it “???”, see [A, table on p. 20]. I believe what is called weakest precondition in this post is often called weakest liberal precondition. So in the terminology of [A], the ??? triples would be defined by wlp(c, post) subset-equal pre.

    [A] Zhang & Kaminski. Quantitative Strongest Post. OOPSLA 2022. https://dl.acm.org/doi/pdf/10.1145/3527331

Leave a comment